Als je ergens met een driehoek werkt met een rechte hoek erin, is het eenvoudig om de raaklijn te vinden, zolang je maar de lengte van twee zijden van de driehoek weet.
Dit is nog eenvoudiger in Microsoft Excel omdat er ingebouwde functies zijn die u kunt gebruiken.
De informatie in dit artikel is van toepassing op Excel voor Microsoft 365, Excel 2019, 2016, 2013, 2010 en Excel voor Mac.
Wat is de raakhoek?
Een raaklijn is een hoek in de driehoek waarvan je de lengte weet van de zijde tegenover de hoek en de zijde ernaast.
Stel je bijvoorbeeld voor dat je baas je vertelt een ladder op precies 70 graden van de grond af te stellen. Tenzij je speciaal gereedschap hebt, zou het ingewikkeld zijn om te meten of de hoek tussen de ladder en de grond precies 70 graden is.
Als je echter een meetlint hebt, kun je de afstand van de onderkant van de ladder tot de muur meten. Aangezien de ladder tegen de muur een driehoek vormt, is dit de zijde die aangrenzend is aan de raakhoek die u probeert te berekenen.
Vervolgens zou je de afstand meten van de onderkant van de muur tot waar de bovenkant van de ladder hem raakt. Dit is de afstand van de zijde die tegenovergestelde is vanaf de raakhoek.
Met de meting van de tegenoverliggende en aangrenzende zijden, kunt u de hoek aan de ladderbasis berekenen met behulp van de boogtangensfunctie.
Als de muur (overzijde) 10 voet is, en de grond (aangrenzende) zijde is 5 voet, dan is de formule voor de raakhoek de overstaande zijde gedeeld door de aangrenzende zijde. Dit is 10 gedeeld door 5, of 0,5.
Om de waarde voor de hoek te vinden, moet je de arctangens van 0,5 nemen.
Zoek de raakhoek met Excel
Je zou een rekenmachine kunnen vinden die de boogtangens van een waarde berekent, maar Excel heeft een ingebouwde functie genaamd ATAN die je kunt gebruiken.
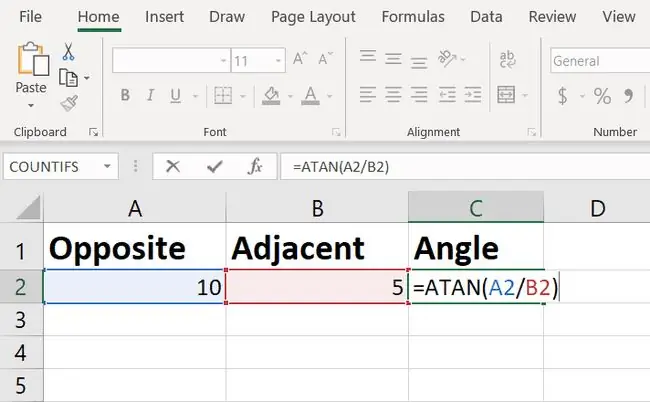
De formule retourneert de hoek in radialen, wat je baas waarschijnlijk niet zal begrijpen.
U wilt radialen converteren naar graden door deze te vermenigvuldigen met 180/pi. Excel heeft ook een PI-functie die u hiervoor kunt gebruiken.
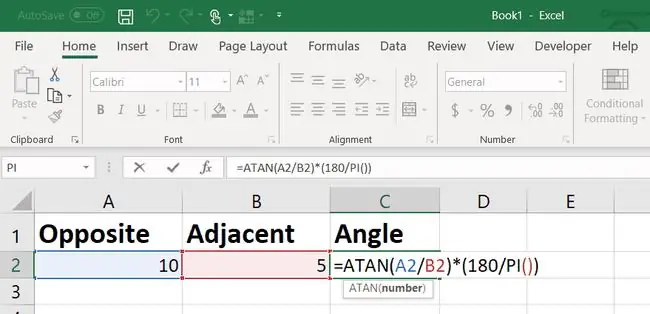
Het antwoord is in dit geval 63,43 graden. Dit betekent dat u een van de lengtes moet aanpassen totdat de hoek precies 70 graden is.
Dit is gemakkelijk te doen in Excel, omdat je de waarde van de andere kant kunt wijzigen totdat het arctangens-resultaat 70 is.
ASIN en ACOS gebruiken in Excel
Laten we in hetzelfde scenario zeggen dat je geen meetlint hebt dat lang genoeg is om de muur te meten. Je weet alleen dat de ladder 15 voet is en dat hij anderhalve meter van de muur is geplaatst.
Excel heeft nog twee andere functies die u kunt gebruiken om de hoek te berekenen.
De lengte van de ladder is de hypotenusa van de driehoek, en de grondafstand is de aangrenzende zijde van de hoek. Zolang de driehoek één rechte hoek (90 graden) heeft, bepa alt de informatie die je hebt de formule die je moet gebruiken.
- Cosinus: Bereken de cosinushoek als je de lengte van de hypotenusa en de aangrenzende zijde kent.
- Sinus: Bereken de sinushoek als je de lengte van de hypotenusa en de tegenoverliggende zijde kent.
In dit geval is de hoek de arccosinus van de aangrenzende zijde gedeeld door de hypotenusa.
Omdat je weet dat de aangrenzende zijde (de grondafstand) 5 voet is en de ladderlengte (hypotenusa) 15 voet is, is de cosinus van de hoek 5 gedeeld door 15, of 0,333.
Gebruik de arccosinus-formule in Excel om de hoek te berekenen.
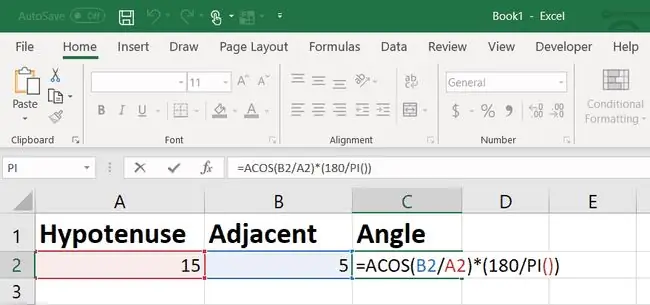
Het resultaat van de arccosinusfunctie is dat Excel in radialen is, dus je moet het vermenigvuldigen met 180/PI om het om te zetten in graden.
Voor een ladder van 15 voet met de basis 5 voet van de muur, is de hoek 70,53 graden.
Als je wist dat de hoogte van de muur (de andere kant) 10 voet is, in plaats van de grondafstand van de muur (de aangrenzende kant), zou je de boogsinus-formule in Excel gebruiken.
In dit geval is de sinus van de hoek de andere kant gedeeld door de hypotenusa.
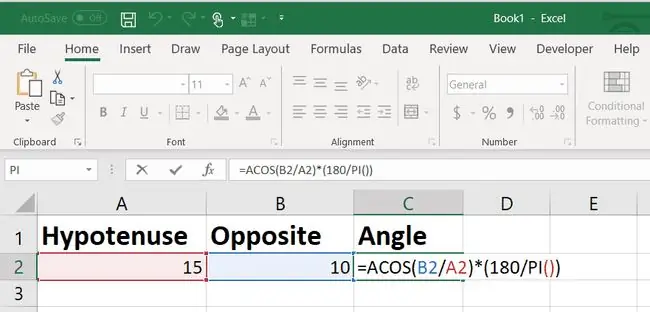
Na conversie naar graden zou de hoek in dit geval 48,12 graden zijn.
Waarom ATAN, ACOS of ASIN gebruiken?
Hier zijn een paar voorbeelden van situaties waarin u mogelijk een van deze functies in Excel moet gebruiken:
- In timmerwerk en constructie worden hoeken en lengtes gebruikt in alle aspecten van het bouwen van huizen en gebouwen.
- Fotografen gebruiken hoeken om de belichting en hun creatieve opnamen zorgvuldig uit te lijnen.
- In de sport kan het begrijpen van hoeken de vaardigheden en de strategie verbeteren.
- Schepen en vliegtuigen worden op radar gelokaliseerd met behulp van hoeken en afstanden.
- Als je zeker wilt weten dat meubels precies in je kamer passen, moet je weten hoe je lengtes en hoeken kunt berekenen.
Je kunt deze berekeningen misschien uitvoeren op een wetenschappelijke rekenmachine. Maar als u er geen bij de hand hebt, kan Excel u helpen die berekeningen te maken.
